이번 포스트에서는 Anomaly Detection에 대해 소개해보고자 합니다. Anomaly detection(이상탐지) 알고리즘은 주어진 샘플에 대한 정상 여부를 판별하기 위한 알고리즘 입니다. 예를 들어 신용카드 사기 여부(credit card fraud detection)나, CCTV와 같은 비디오 감시(video surveillance), 자율 자동차 주행(autonomous driving)과 같은 다양한 분야에서 사용될 수 있으며, 특히 마키나락스가 집중하고 있는 산업(제조업)에서는 장비 이상 탐지, 불량 제품 탐지와 같은 중요한 문제를 해결할 수 있습니다. 하지만 anomaly detection의 중요성에 비해 이에 대한 연구는 아직 활발하지 않습니다.
앞으로의 포스팅에서는 딥러닝을 활용한 anomaly detection과 마키나락스가 개발한 RaPP 방법에 대해서도 다루도록 하겠습니다. 또한, 오토인코더 이외의 다양한 방법들을 활용한 anomaly detection 방법들에 대해서도 리뷰하도록 하고자 합니다.
Motivations
사실 이상 또는 비정상을 탐지하는 것은 단순한 binary classification(이진 분류)문제로 생각해 볼 수 있습니다. Binary classification에 대한 방법들은 잘 알려져 있으며, 딥러닝을 통해서도 쉽게 구현이 가능합니다. 하지만 기존의 전형적인 분류 알고리즘들은 다음과 같은 이유들로 인해서 적용될 수 없습니다. 앞으로 서술할 내용들은 [1]에서도 살펴보실 수 있습니다.
Highly imbalanced data
실제 세상에서 우리는 당연히 정상 데이터를 비정상 데이터에 비해서 훨씬 쉽게 얻을 수 있습니다. 즉, 비정상 데이터는 정상 데이터에 비해서 매우 적게 수집될 가능성이 높습니다. 이렇게 수집된 불균형한 데이터셋(imbalanced dataset)을 통해 딥러닝(머신러닝)을 수행하게 된다면, 모델은 각 샘플들에 대해 동등하게 학습하였을때 비정상 데이터에 대한 특징을 잘 배우지 못하게 될 것입니다. 또한 예를 들어 99%의 정상 데이터들로 구성되어 있다고 가정한다면, 시스템은 그냥 아무런 근거 없이도 정상이라고 찍어(guess)버리면 평균적으로 100점 만점에 99점을 받게 될 것입니다. 따라서 이와 같이 극심한 불균형 데이터셋에 대해서 판별하는 모델을 만들고자 할 때, 우리는 anomaly detection 알고리즘을 활용하게 됩니다.
Open-world classification problem
어쩌면 그럼 우리는 99%의 정상 데이터로 가득한 데이터셋을 학습할 때, 비정상을 99배 더 학습하도록 하는 방법도 생각해 볼 수 있을 것 입니다. 하지만 아쉽게도 이 방법을 통해서도 문제를 해결할 수 없습니다. 왜냐하면 대부분의 경우 비정상 데이터는 정상 데이터에 비해서 다양한 패턴을 가질 것 입니다. 하지만 불균형 데이터셋에서도 알 수 있듯이, 우리는 이러한 다양한 특징들을 배우기에는 비정상 데이터의 양이 턱없이 모자랍니다. 게다가 예를 들어 비정상 패턴들을 통해 비정상 클래스를 정의한다고 하면, 우리는 애초에 비정상 클래스가 유한하게 정의될 수 있는지도 알 수 없습니다. 이러한 문제 상태를 open-world classification 이라고 하며, 당연히 그럼 우리는 수집된 비정상 데이터를 통해 모든 비정상 데이터의 패턴을 배울 수 없습니다.
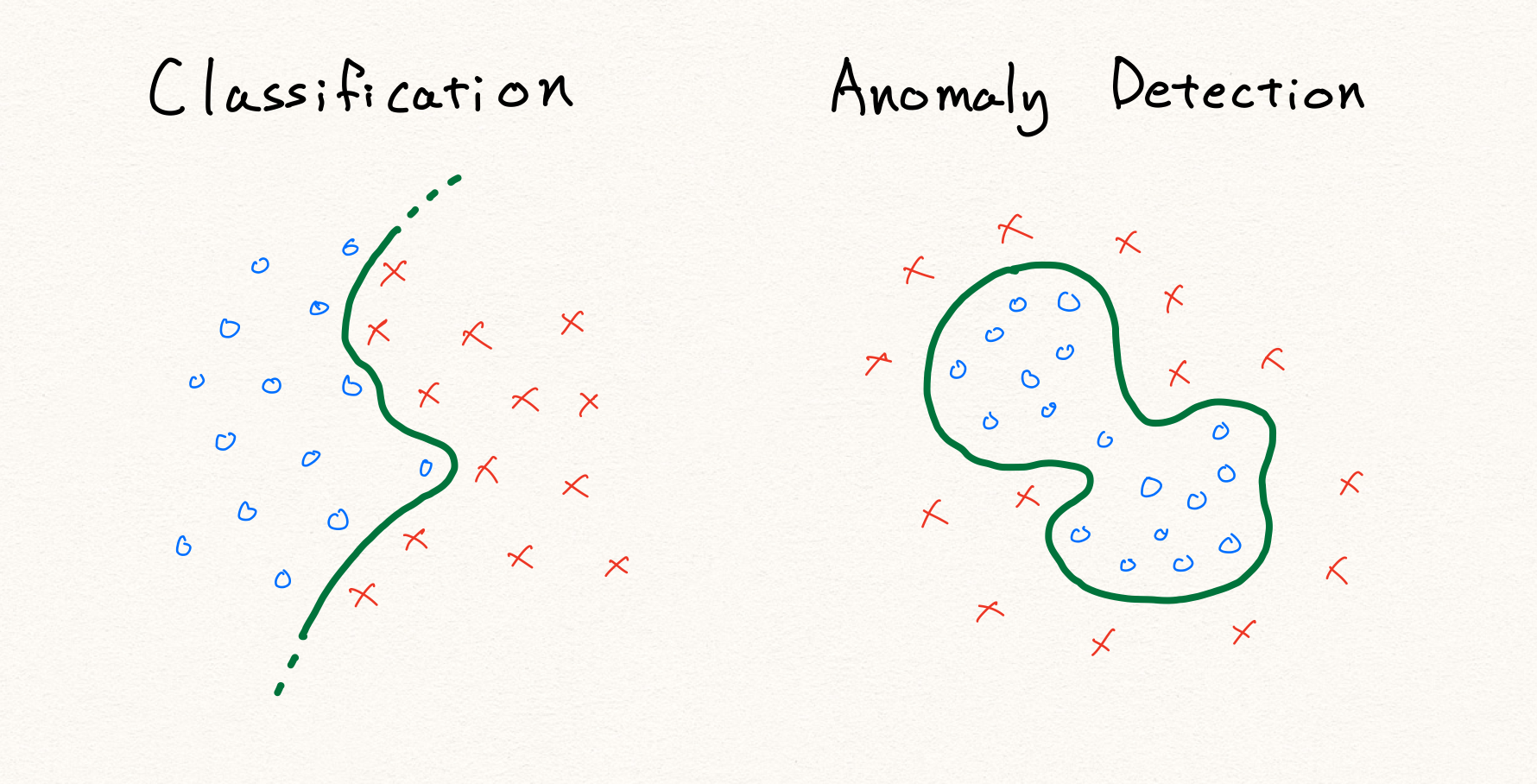
예를 들어 위의 그림과 같이 기존의 분류 문제라면 단순히 정상과 비정상을 가르는 decision boundary를 찾는 문제가 될 것 입니다. 하지만 정의에 따라 anomaly detection에서 비정상 데이터는 정상 영역 이외의 영역에 분포하는 데이터를 가리킵니다. 따라서 위와 같이 단순히 주어진 데이터를 통해 경계선을 찾게 된다면, 학습 데이터 내의 불량 데이터에 대해서만 정상적으로 판별할 수 있는 모델이 될 것 입니다. 결국 우리는 기존의 전형적인 판별 알고리즘을 사용하여 anomaly detection을 구현할 수 없습니다.
Before Deep Learning
딥러닝 이전에도 anomaly detection을 하기 위한 다양한 시도들이 있었습니다. 예를 들어 One-class SVM 또는 Gaussian Mixture Model (GMM)과 같은 알고리즘을 사용하여 정상 데이터의 영역을 정의하거나, 정상 데이터의 분포를 추정하는 방법을 통해 anomaly detection을 수행하였습니다. 특히 kernel-SVM의 경우에는 DNN(deep neural network)를 커널로 사용하여 여전히 사용되기도 합니다.
PCA
그 중에서도 우리는 PCA(주성분 분석)에 대해서 가장 주목하고자 합니다. 앞으로 설명할 오토인코더와 가장 유사한 아이디어로 동작하기 때문입니다. (아마도 PCA가 오토인코더의 특수한 형태라고 설명할 수 있을 것 같습니다.)
PCA는 데이터의 분포에 따라 그 분산을 가장 최대로 하는 축을 찾아냅니다. 우리는 보통 SVD(singular value decomposition)을 통해 PCA를 수행할 수 있습니다. 좀 더 자세한 설명은 SVD에 대한 내용을 찾아보시기 바랍니다.
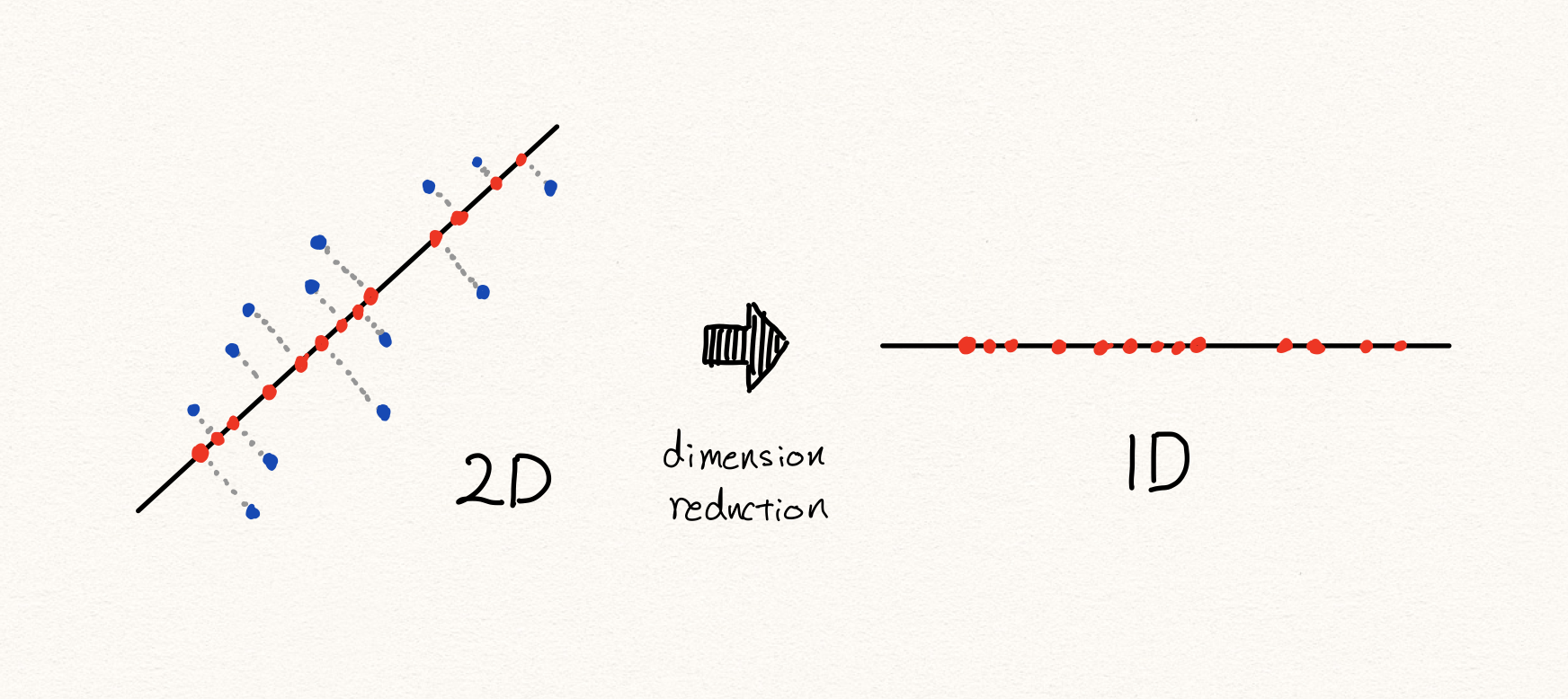
우리는 이처럼 선형적으로 차원을 축소할 수 있습니다. 이때 샘플들은 선택된 축들로 projection(투사)됩니다. 이렇게 낮은 차원의 공간들에 존재하는 샘플들을 다시 원래 높은 차원의 공간으로 복원하게 되었을 때, 차원 축소 전 원래의 샘플의 위치와 비교하여 거리가 먼 샘플은 비정상이라고 판별하게 됩니다.
이를 수식으로 나타내면 다음과 같이 표현할 수 있을 겁니다.
\[
\begin{gathered}
f: x \to \mathbb{R}^n, \text{ where } x \in \mathbb{R}^m, \\
g: \mathbb{R}^n \to \mathbb{R}^m \text{ and } \hat{x} = g \circ f(x), \text{ where } m > n. \\
\\
\text{anomaly\_score}(x) = ||x - \hat{x}||, \\
\text{is\_anomalous}(x) =
\begin{cases}
1, & \text{if anomaly\_score}(x) \ge \tau, \\
0, & \text{otherwise.}
\end{cases}
\end{gathered}
\]
우리는 PCA를 통해 고차원의 공간에서 저차원의 공간으로 맵핑하는 함수를 배울 수 있습니다. 이후에 다시 복원된 값과 원본 값을 비교하여 차이가 작을수록 정상이다라고 할 수 있습니다.
Discussion
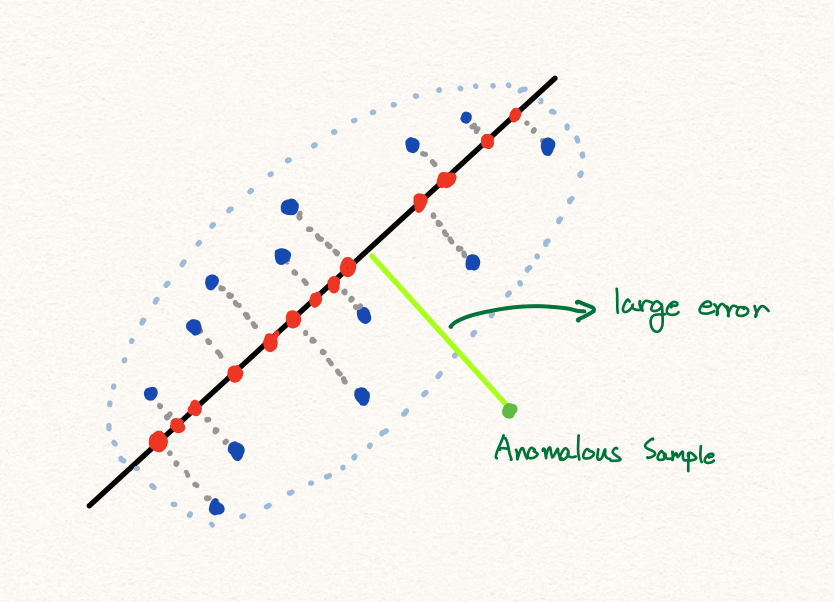
이와 같이 PCA를 통해 우리는 anomaly detection을 수행할 수 있습니다. 하지만 많은 경우에 PCA는 훌륭하게 동작하지만, 아래와 같은 경우에는 잘 동작하지 않을 수 있습니다.
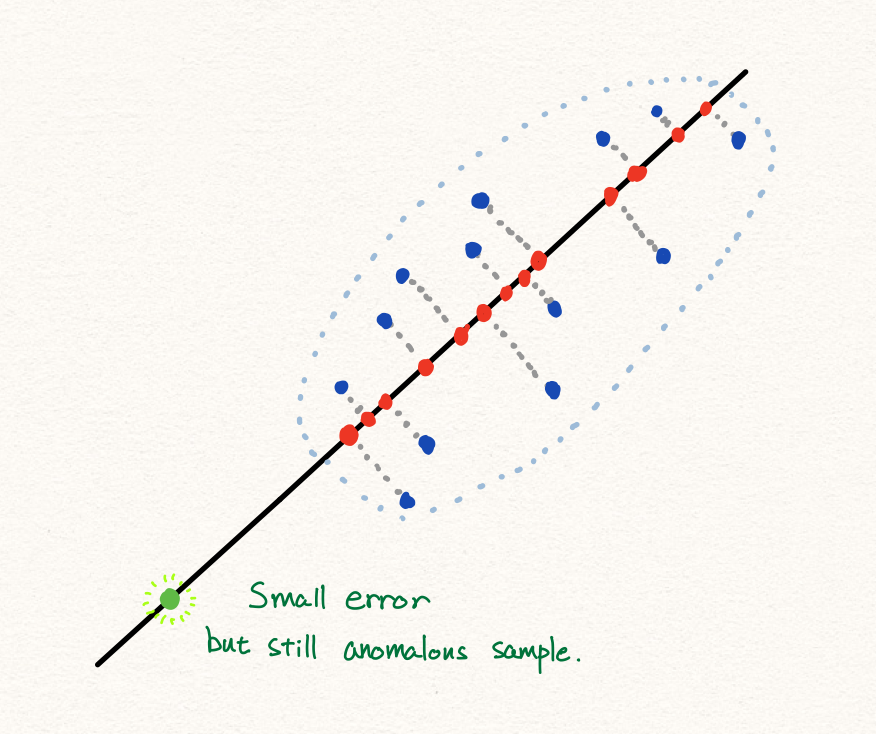
또한 만약 데이터의 분포가 아래와 같다면, 선형적인 축소 방식으로 인해서 우리는 PCA를 통해 성공적인 anomaly detection을 수행하지 못할 것 입니다. 따라서 우리는 딥러닝을 통해 비선형적인 데이터에 대해서 anomaly detection을 수행하고자 합니다.
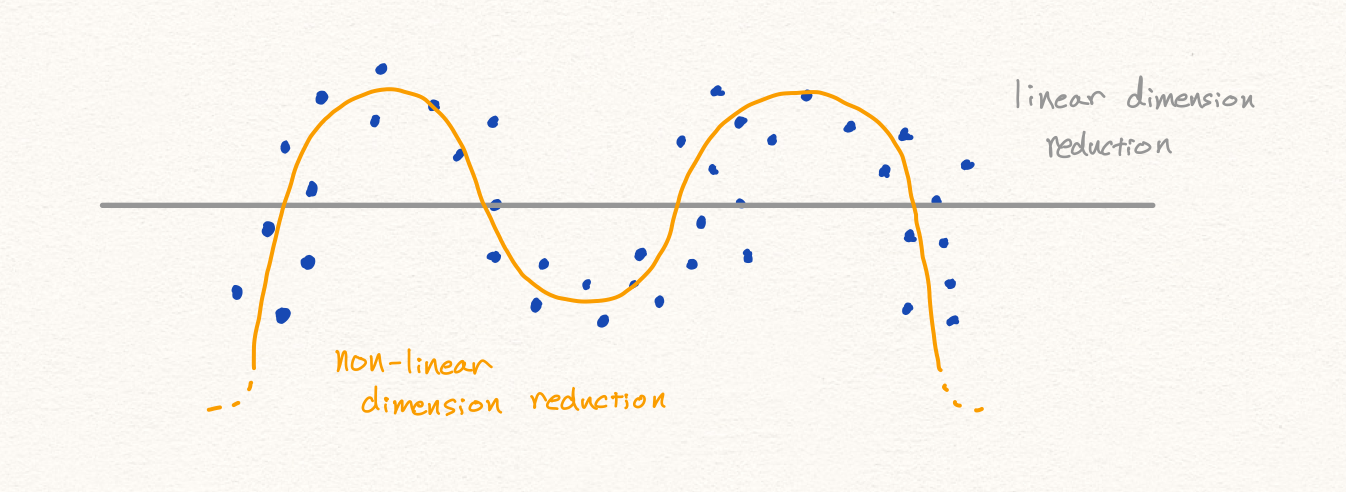
Problem Setups in Anomaly Detection
비록 anomaly detection에 대해서 활발한 연구가 부족하지만, 문제를 정의하는 다양한 방법들이 존재합니다. 따라서 입문자들이 느끼기에는 다소 혼란스러울 수 있습니다. 이번 섹션에서는 다양한 anomaly detection에 대한 문제 정의와 실험 환경 셋팅에 대해서 이야기 하고자 합니다.
Out-of-distribution
먼저 computer vision 분야에서 활발하게 연구되고 있는 주제입니다. 예를 들어 MNIST를 대상으로 학습된 이미지 분류 네트워크가 있다고 가정해 보겠습니다. 이 네트워크는 매우 성능이 좋아서 MNIST 클래스에 대한 성공적인 예측을 잘 수행합니다. 만약 이 네트워크에 MNIST와 똑같은 크기의 사람 얼굴 사진을 넣으면 어떤 예측이 나올까요? 그 네트워크는 뭔가를 예측할 것이고, 예를 들어 얼굴이 동그란 모양이니 우연히 0에 대해서 높은 softmax 결과값으로 예측했다고 해보죠. 그럼 우리는 과연 네트워크의 그 값을 믿어야 할까요? 신경망은 학습데이터의 도메인에 대해서만 학습이 되었기 때문에, 학습데이터 영역 밖의 데이터가 주어지면 어떻게 동작할지 전혀 알 수 없습니다. 또한 이러한 경우에 출력된 값은 믿을 수 없을 것 입니다. OOD(Out-of-distribution) 문제는 이러한 문제를 해결하고자 합니다.
이를 위해서 OOD는 보통 학습한 데이터와 다른 데이터셋이 주어졌을 때, 이것을 판별해내는 것입니다. 보통 OOD 알고리즘을 평가하기 위해서는 두 개 이상의 데이터셋이 있을 때, 하나의 데이터셋만을 학습한 신경망에 학습에 참여하지 않은 데이터셋이 주어지는 형태로 실험이 진행 됩니다. 즉, MNIST를 학습한 신경망에 MNIST와 F-MNIST가 주어진다면 신경망이 이를 구분해 낼 수 있는지 여부가 중요하게 적용됩니다. (한마디로 데이터셋 분류기랄까요?) 결과적으로 우리는 이미지 분류기를 통과하기에 앞서, 주어진 입력을 OOD 모델을 통해 적합한지 따져볼 수 있을 것 입니다. – 추가로 OOD는 adversarial attack과 연관지어 연구가 이루어지기도 합니다. [3, 4]
Semi-supervised Anomaly Detection
다음은 마키나락스가 주로 다루는 주제에 대해 소개하고자 합니다. 보통 anomaly detection이라하면 이 문제에 대해서 이야기 하는 것 입니다. [6] 널리 사용되는 만큼 이외에도 outlier detection, novelty detection [5] 과 같은 다양한 이름을 갖고 있습니다.
이 문제는 아래와 같은 방법을 통해 학습과 평가가 진행됩니다. 먼저 모델을 학습할 때에는 정상 데이터만을 갖고 학습합니다. 그럼 학습이 완전히 종료된 이후에 테스트 과정에서 비정상 데이터가 주어졌을 때, 모델이 정상인지 비정상인지 판별할 수 있는지 여부가 가장 중요한 평가 요소입니다. 어쩌면 OOD와 거의 유사한 형태로 진행되는 것을 볼 수 있습니다. 다만 이 주제과 OOD의 차이점은 보통 동일한 데이터셋(또는 연관있는 데이터셋)내에서 이루어진 다는 점이며, 크게 아래와 같은 두 가지 케이스로 진행됩니다.
Unimodal normality case
먼저 우리는 정상의 패턴이 하나이고, 비정상 패턴이 다양한 형태를 상상해 볼 수 있습니다. 예를 들어 MNIST의 경우에 임의의 숫자 클래스 하나를 정상 데이터로 가정하고 학습을 진행합니다. 이후에 테스트 과정에서 10가지 클래스 모두를 포함하여 모델이 정상 클래스와 비정상 클래스를 잘 구별하는지 테스트할 수 있을 것입니다. 이 케이스는 one-class classification [7] 이라는 이름으로도 널리 알려져 있습니다.
Multimodal normality case
근데 사실은 어쩌면 정상 또한 다양한 패턴으로 나타날 수 있을 것 입니다. 예를 들어 우리가 자동차 엔진에 대해서 anomaly detection을 수행한다고 하였을 때, 엔진은 4가지의 다른 상태(흡기, 압축, 폭발, 배기)로 정의 될 수 있고, 각 상태는 서로 꽤 상이할 수 있습니다. 따라서 우리는 정상 데이터가 단순히 한 가지라고 가정하고 문제에 접근하는 것은 상황에 따라 옳지 않은 방법이 될 수 있습니다.
이 문제에 대한 모델을 학습하고 평가하기 위해서는 다음과 같은 과정이 필요합니다. 예를 들어 MNIST 9개의 클래스를 임의로 정상 데이터로 가정한다면, 9가지 클래스를 통해 모델 학습을 진행합니다. 학습이 종료된 이후에, 나머지 비정상으로 간주된 1개의 클래스를 합쳐 전체 10개의 클래스를 통해 정상 클래스와 비정상 클래스를 분류해내는지 평가합니다. 보통은 앞서 설명한 unimodal normality case에 비해서 어려운 setup으로 취급되고, 따라서 모델도 더 낮은 성능을 보이게 됩니다.
비록 우리는 모델을 학습할 때에는 비정상 데이터를 보여주지 않지만 정상데이터만 넣어주어야 한다는 점에서, 수집된 데이터들을 정상 데이터와 비정상 데이터로 레이블링 해야 하며 이와 같은 이유 때문에 semi-supervised learning 방식에 속하는 것이라고 볼 수 있습니다.
우리 마키나락스는 주로 이 방법에 대해서 연구를 수행하며, novelty detection이라는 이름으로 부르고 있습니다. 그 이름에서 볼 수 있듯이, 데이터의 참신성(novelty)을 탐지하기 위한 방법임을 알 수 있습니다. 좀 더 자세한 셋업은 ICLR 2020에 출판된 마키나락스의 페이퍼 RaPP[5] 를 참고하세요.
Unsupervised Anomaly Detection
그럼 우리는 수집된 데이터들이 정상 또는 비정상 레이블링이 전혀 없는 경우에 대해서도 생각해 볼 수 있을 것입니다. [8] 수집된 데이터를 일괄적으로 학습용과 평가용으로 나눈 후에 모델 학습과 평가를 진행할 수 있겠지요. 이와 같은 방법을 unsupervised anomaly detection이라고 부릅니다. 이 경우에도 마찬가지로 unimodal normality case와 multimodal normality case로 나눠볼 수 있을 것입니다.
아쉽게도 anomaly detection에 대한 집중적인 연구가 이루어지지 않은 덕분에 위의 문제 정의들에 대한 약간의 차이가 있을 수 있습니다. 예를 들어 semi-supervised anomaly detection 또는 novelty detection을 unsupervised anomaly detection으로 부르기도 합니다. 따라서 논문을 접할 때 문제 setup에 대해서 유의하며 읽어야 합니다.
Evaluations
기존의 분류 알고리즘을 사용할때는 보통 해당 클래스에 속할 확률(또는 likelihood)값을 얻게 되어, 각 클래스별 확률값 비교를 통해 가장 높은 확률을 갖는 클래스를 선택하게 됩니다. 하지만 anomaly detection의 경우에는 (supervised learning에 기반하지 않기 때문에) 클래스별 확률값이 아닌, 샘플 자체에 대한 anomaly score가 주어지는 경우가 많습니다. 따라서 anomaly score에 대한 threshold 설정이 필요합니다.
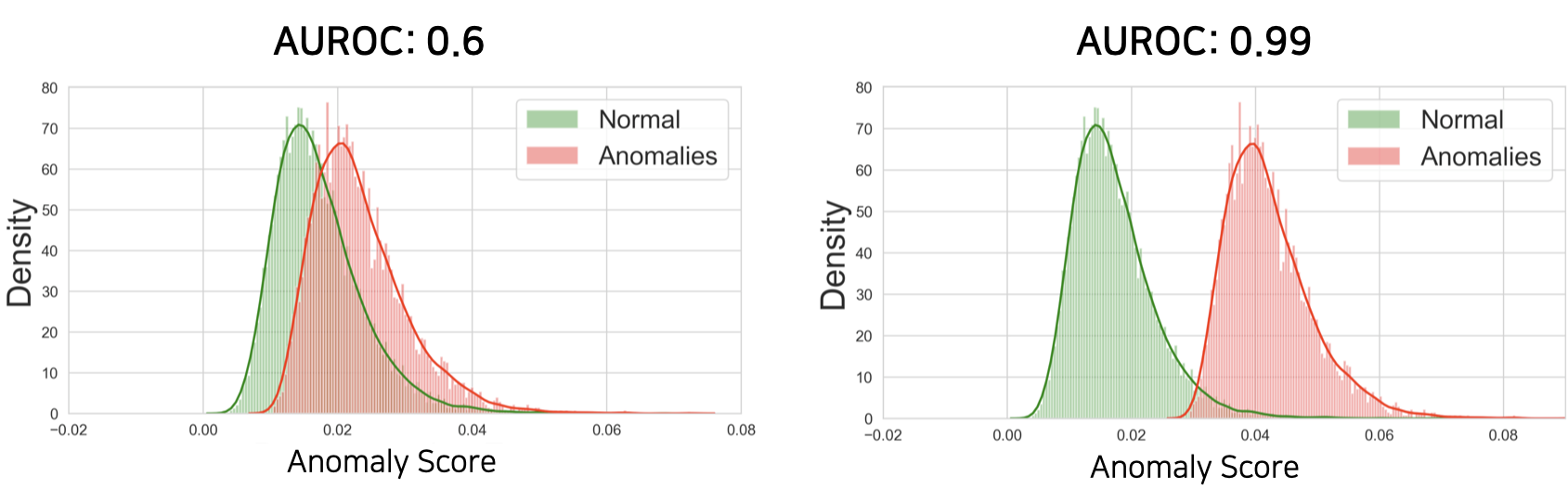
예를 들어 우리는 테스트 데이터셋에 대해서 위와 같이 anomaly score들을 구하여 anomaly score의 분포로 만들어 볼 수 있습니다. 이때 두 분포가 충분히 겹쳐있지 않다면, 두 분포 사이를 잘 가로지르는 threshold를 설정할 수 있습니다. 하지만 물론 우리는 테스트셋을 실제로는 볼 수 없기 때문에 이와 같이 threshold를 구하는 것은 어렵고, 보통은 학습 데이터의 정상 데이터의 분산의 크기를 보고 결정하기도 합니다.
어쨌든 우리는 정상 데이터의 anomaly score 분포와 비정상 데이터의 anomaly score 분포가 겹쳐있는 부분이 적을수록 threshold를 정하는 작업이 굉장히 수월해질것 입니다. 왜냐하면 만약 두 분포가 정말 멀리 떨어져있다면, 적당히 대충 threshold를 정해도 두 분포를 잘 갈라낼 것이기 때문입니다. — robust한 알고리즘이라고 할 수 있습니다. 따라서 보통 우리는 두 분포의 분리의 정도를 측정하는 방법인 AUROC를 통해 anomaly detection 성능을 측정합니다. (가끔 AUPR을 통해서도 anomaly detection 성능을 측정합니다.)
앞서 언급한대로 PCA의 경우에는 reconstruction error(원본값과 복원값의 차이의 크기)를 anomaly score로 삼아 점수가 큰 경우에 비정상으로 간주합니다. 즉, 복원이 잘 되지 않는 샘플일수록 비정상으로 간주합니다.
Deep Anomaly Detections
예전부터 위와 같은 문제 정의들을 통해서 연구가 이루어져왔고, 당연히 딥러닝의 눈부신 성과에 힘입어 딥러닝을 통해 anomaly detection을 해결하고자 하는 시도들이 이어지고 있습니다. 우리는 크게 4가지 알고리즘으로 나눠 볼 수 있습니다.
Deep-kernel-based Anomaly Detections
Kernel-SVM과 같이 기존의 커널 기반 머신러닝 알고리즘에 Deep Neural Networks (DNN)을 활용한 커널을 사용하는 방식입니다. 이 포스트에서는 자세히 다루지 않도록 합니다.
Auto-encoder based Anomaly Detections
오토인코더는 PCA처럼 차원축소를 통해 피쳐를 추출해내지만, 그것을 비선형적으로 수행한다는 점에서 큰 차이가 있습니다. (오토인코더의 non-linear activation function을 없애고 학습하면 PCA와 비슷하게 동작합니다.) 오토인코더는 쉽게 말해 압축과 해제를 하며 피쳐를 추출합니다. 예를 들면, MP3의 경우에는 일반적인 사람이 듣기에는 실제 음원과 큰 차이가 없지만, 용량에서는 큰 차이를 보입니다. 이는 사람이 잘 듣지 못하는 주파수 영역의 데이터는 날려버리고, 실제로 중요한 주파수 영역만 압축했기 때문입니다. — 손실 압축을 수행합니다. 마찬가지로 오토인코더도 주어진 고차원 공간상의 샘플을 bottle-neck(병목) 구간의 저차원 공간으로 맵핑하는 방법을 학습하는 과정에서 (이를 다시 고차원 공간으로 복원해야 하기 때문에) 복원에 필요없는 정보부터 버리게 될 것 입니다.
이처럼 오토인코더는 인코딩(encoding)과 디코딩(decoding) 과정을 통해서 스스로 특징(feature)을 추출하는 방법을 배웁니다. 하지만 MNIST에 대한 복원 결과를 보면 알 수 있듯이, 보통은 blur 하게 복원되는 특징이 있습니다. 이는 MSE 손실 함수를 사용했기 때문이라고 볼 수 있습니다. MSE 손실 함수는 불확실한 부분에 대해서는 평균값으로 예측하도록 동작하기 때문입니다. 추가로 우리는 단순한 오토인코더 뿐만 아니라 다양한 오토인코더(e.g. VAE, AAE) 등을 활용하여 anomaly detection을 구할 수 있습니다. — 데이터셋에 따라 VAE와 AAE가 더 뛰어난 성능을 보이기도 합니다. [2, 5, 6]
따라서 PCA와 같이 복원된 샘플에 대해서 원본 샘플과의 차이를 비교하는 방식인 reconstruction error based anomaly detection 에서는 성능이 떨어질 우려가 있습니다.
Generative Adversarial Network based Anomaly Detections
복원 오차에 기반한 anomaly detection 방식에서 MSE 손실함수의 사용으로 인한 복원 성능 하락은 anomaly detection 성능에 영향을 끼칠 수 있습니다. 따라서 오토인코더 기반 방식의 단점을 보완하기 위해 제안된 방법은 GAN을 활용하여 anomaly detection을 수행하는 것입니다. [9, 10, 11] 하지만 GAN의 경우에는 generator와 discriminator 사이의 적대적 학습을 통해 모델이 학습되기 때문에, 오토인코더와 달리 직접적으로 차원 축소를 수행하는 모듈이 존재하지 않습니다. 이는 GAN이 사실은 주로 생성 자체를 위한 모델이고, 차원 축소를 위한 모델은 아니기 때문입니다. 하지만 anomaly detection은 테스트 과정에서 샘플이 주어지면 이를 차원 축소 이후에 복원하는 과정을 거쳐야 하기 때문에, 차원 축소를 위한 모듈이 필요합니다.
따라서 기존의 GAN 기반의 anomaly detection 방법들은 이를 해결하기 위한 여러가지 방법들을 제시하였습니다. 예를 들어 AnoGAN [9]의 경우에는 이를 해결하기 위해서 generator로부터 생성된 \(\hat{x}\) 과 \(x\) 와의 차이를 최소화하는 latent variable \(z\) 를 찾도록 back-propagation을 수행하는 방법을 수행합니다. — 추후 GAN에 대한 anomaly detection 포스트를 다루도록 하겠습니다.
아쉽게도 MSE의 단점을 보완하고자 제안된 GAN의 경우에는 CNN에서만 동작할뿐더러, generator와 discriminator의 균형있는 학습도 굉장히 큰 장애물로 작용합니다. 또한 reconstruction error가 낮다고 무조건 모델의 성능이 좋은 것도 아님을 실험적으로 알 수 있었으므로, 마키나락스는 주로 오토인코더에 기반한 anomaly detection을 수행합니다.
Self-supervised Learning based Anomaly Detections
가장 최근에 제안된 방법으로, 학계에서 주목받고 있는 self-supervised learning 기법을 활용하여 anomaly detection에 적용하였습니다. 물론 오토인코더도 주어진 입력을 똑같이 복원하도록 학습한다는 점에서, self-supervised learning에 속할 수 있습니다. 하지만 여기서 소개하고자 하는 방법들은 좀 더 다양한 objective를 수행하도록 학습시킨다는 점에서 다릅니다.
예를 들어 2018년 NIPS에서 제안된 논문인 Deep Anomaly Detection Using Geometric Transformations [12] 에서는 주어진 이미지에 대해서 미리 정의한 변형(transformation)을 준 이후에, 네트워크가 변형의 종류를 맞추도록 학습시킵니다. 그럼 테스트 과정에서 비정상 샘플에 변형이 추가되었을 때, 네트워크는 어떤 변형이 추가되었는지 잘 맞추지 못할 것입니다. 이 논문은 비록 변형 방법이 이미지에 국한되지만, 새로운 방법을 제시한 논문으로 주목 받았습니다.
Summary
이번 포스트에서는 anomaly detection에 대해 소개하고, 다양한 문제 정의와 이를 해결하기 위한 딥러닝 알고리즘들을 소개하였습니다. 추후 이어질 포스팅에서는 각각의 알고리즘에 대해서 좀 더 자세히 소개하고자 합니다.
References
- [1] Ki Hyun Kim, Operational AI: Building a Lifelong Learning Anomaly Detection System, DEVIEW, 2019
- [2] Jinwon An et al., Variational Autoencoder based Anomaly Detection using Reconstruction Probability, SNU Data Mining Center, 2015
- [3] Anh Nguyen et al., Deep Neural Networks are Easily Fooled: High Confidence Predictions for Unrecognizable Images, CVPR, 2015
- [4] Ian J. Goodfellow et al., Explaining and Harnessing Adversarial Examples, Arxiv, 2014
- [5] Ki Hyun Kim et al., RaPP: Novelty Detection with Reconstruction along Projection Pathway, ICLR, 2020
- [6] Stanislav Pidhorskyi et al., Generative Probabilistic Novelty Detection with Adversarial Autoencoders, NeurIPS, 2018
- [7] Lukas Ruff et al., Deep One-Class Classification, ICML, 2018
- [8] Siqi Wang et al., Effective End-to-end Unsupervised Outlier Detection via Inlier Priority of Discriminative Network, NeurIPS, 2019
- [9] Thomas Schlegl et al., Unsupervised Anomaly Detection with Generative Adversarial Networks to Guide Marker Discovery, Arxiv, 2017
- [10] Houssam Zenati et al., Efficient GAN-Based Anomaly Detection, Arxiv, 2018
- [11] Ilyass Haloui et al., Anomaly detection with Wasserstein GAN, 2018
- [12] Izhak Golan et al., Deep Anomaly Detection Using Geometric Transformations, NeurIPS, 2018
» 이 글은 마키나락스 미디엄에 게재된 포스팅으로 원문은 여기서 확인하실 수 있습니다.
