Neural Combinatorial Optimization은 딥러닝을 사용하여 조합 최적화 문제(Combinatorial Optimization Problem)를 풀고자 하는 연구분야입니다. 이번 포스팅에서는 그 중에서도 조합 최적화 문제의 풀이에 강화학습의 사용을 제안한 대표적인 연구[1]를 소개하려고 합니다.
Combinatorial Optimization Problem
조합 최적화 문제란 유한한 탐색공간(search space)에서 최적의 해를 찾는 문제이며, 그 탐색공간은 보통 이산적(discrete)으로 표현할 수 있습니다. 대표적인 문제로는 순회 세일즈맨 문제 (Traveling Salesman Problem), 작업공정 스케줄링 (Job Ship Scheduling), 배낭 문제 (Knapsack Problem) 등이 여기에 해당하며, 많은 조합 최적화 문제들이 NP-Hard 군에 속하는 것으로 알려져 있습니다. 이 중 “순회 세일즈맨 문제”에 대해 좀 더 자세히 살펴보도록 하겠습니다.
Traveling Salesman Problem (TSP)
순회 세일즈맨 문제(이하 TSP)는 여행거리의 총합이 최소화되도록 전체 노드의 순회순서를 결정하는 문제입니다. 아래 그림처럼 노드의 순회순서를 결정함에 따라 전체 여행거리의 총합은 천차만별로 달라질 수 있습니다.
 [그림1] 주어진 노드에 대한 두 개의 솔루션 비교 [2]
[그림1] 주어진 노드에 대한 두 개의 솔루션 비교 [2]
이는 N개 지점에 대한 모든 순열(Permutations)을 탐색하는 문제로, Brute-Force Search의 경우 $O(N!)$, Dynamic Programming의 경우 $O(N^2 2^N)$의 계산복잡도를 보이는 NP-Hard 문제입니다 [3]. 보통 많은 개수의 노드에 대한 솔루션을 구해야 할 때는 적절한 휴리스틱(Heuristic)을 사용하여 탐색공간을 줄이는 방식으로 계산 효율을 높이곤 합니다 [4]. 하지만 휴리스틱을 사용하는 경우 문제의 세부사항이 변경되면 휴리스틱 또한 적절히 수정해야 하는 번거로움이 발생합니다. 2016년 말, 이 문제의식에 의거한 연구의 성과가 Google Brain의 연구진들로부터 공개되었습니다
Neural Combinatorial Optimization with Reinforcement Learning (2016)
Neural Combinatorial Optimization with Reinforcement Learning[1]의 저자들은 별도의 휴리스틱(Heuristic)의 정의 없이도 2D Euclidean Graphs로 표현된 (최대 100개 노드의) TSP를 푸는 새로운 방법을 제안합니다. 딥러닝을 사용하여 TSP 문제의 학습이 가능함을 보였던 Pointer Network[7]가 지닌 지도학습(Supervised Learning)의 한계점을 강화학습을 통해 개선하려는 것이 주요한 아이디어라 할 수 있습니다. 이러한 접근은 강화학습으로 Neural Architecture Search라는 이산문제를 풀었던 이전 연구경험[5]에서 기인한 것으로 보여집니다.
“We empirically demonstrate that, even when using optimal solutions as labeled data to optimize a supervised mapping, the generalization is rather poor compared to an RL agent that explores different tours and observes their corresponding rewards.”
Pointer Network
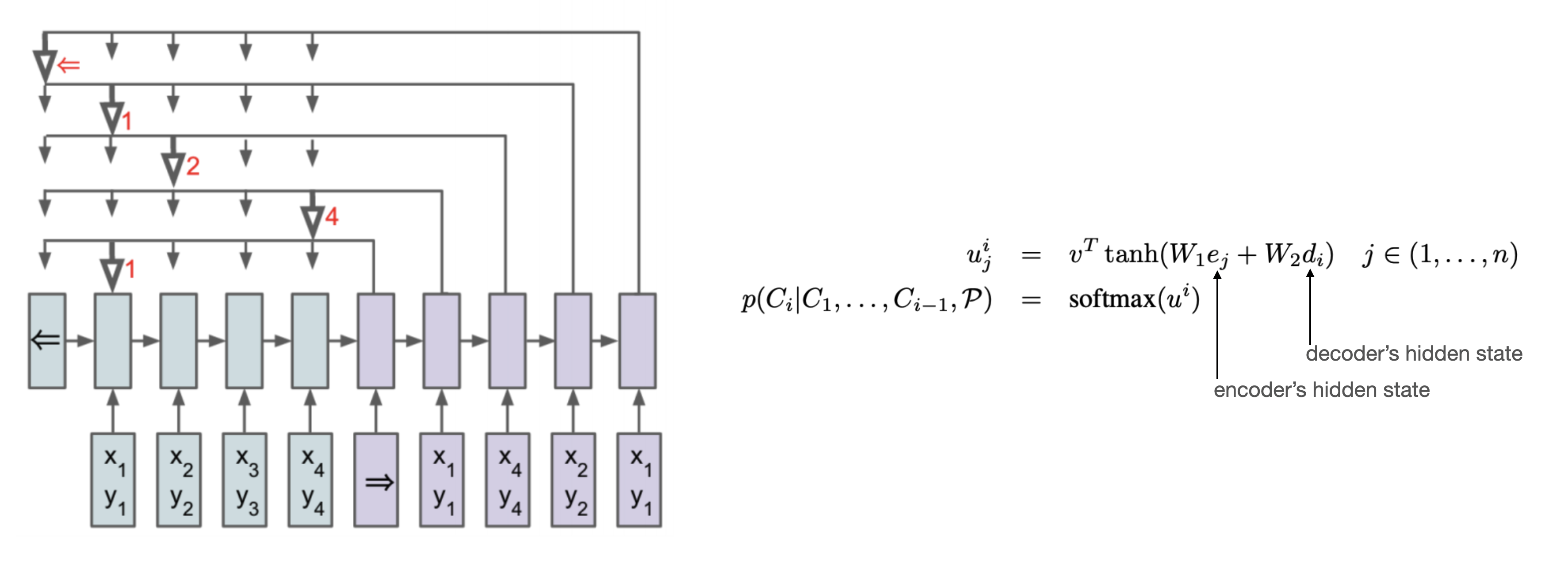 [그림2] Pointer Network 구조 [7]
[그림2] Pointer Network 구조 [7]
이 논문에서는 Pointer Network[7]의 기본구조를 그대로 이용합니다. Pointer Network는 임의 개수의 노드에 대해서도 동작할 수 있는 것이 특징입니다. 즉, 상대적으로 적은 노드의 TSP를 학습한 뒤에 (학습데이터에 존재하지 않는) 더 많은 노드의 TSP에 대해서도 동작 가능한 구조입니다.
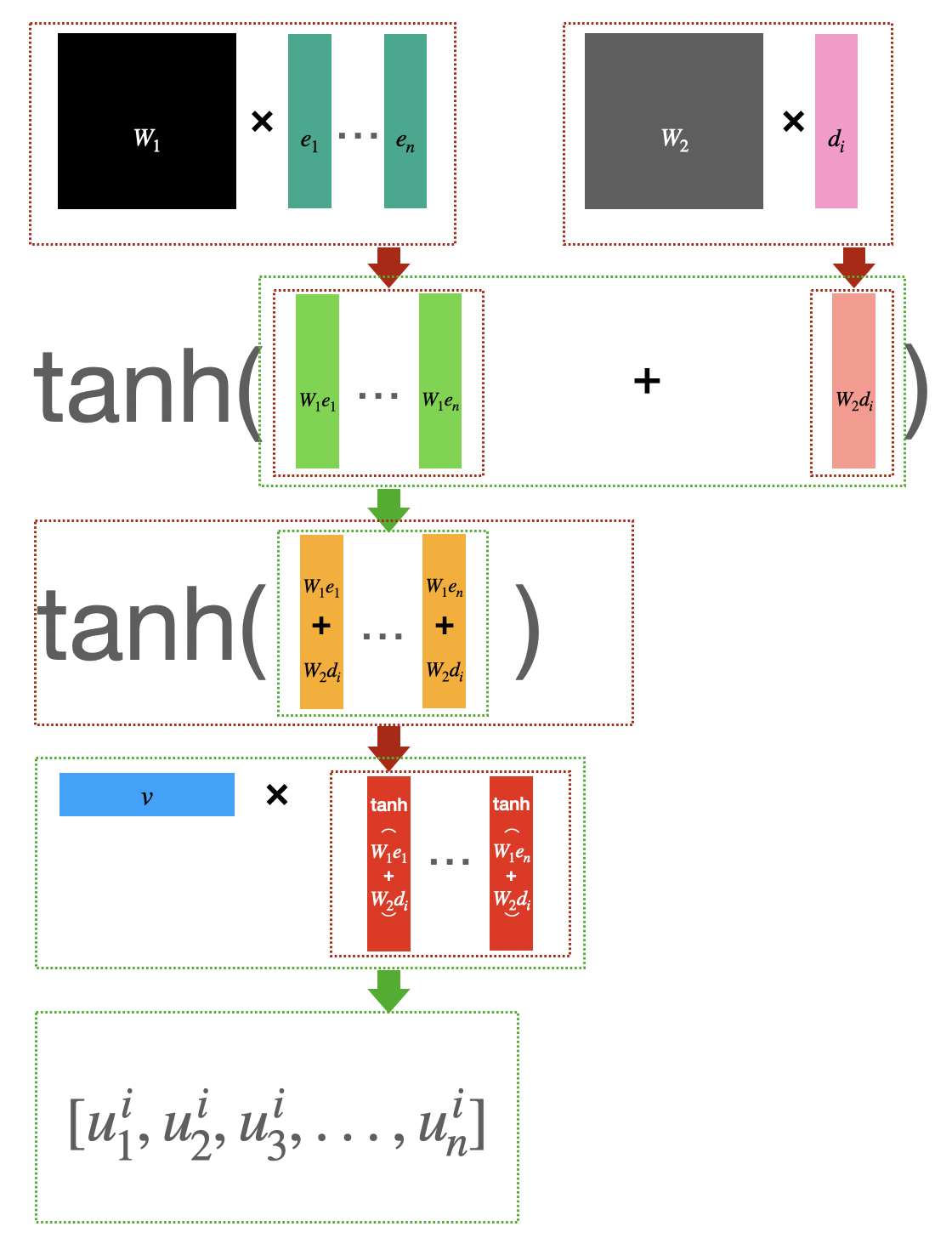 [그림3] u^i의 계산과정 [7]
[그림3] u^i의 계산과정 [7]
Pointer Network는 입력에 대한 Attention Mask($u^i$에 대한 Softmax)를 예측에 바로 사용합니다. Attention Mask의 차원이 입력의 개수에 따른다는 속성을 이용해 같은 크기의 학습파라미터를 가지고도 가변적인 개수의 TSP에 대해 동작하게 할 수 있습니다. 그럼으로써 5~20개 노드에 대한 최적해를 학습하여 그것보다 더 많은 (25~50개) 노드의 TSP에 대해서도 유의미한 성능을 얻어냈습니다.
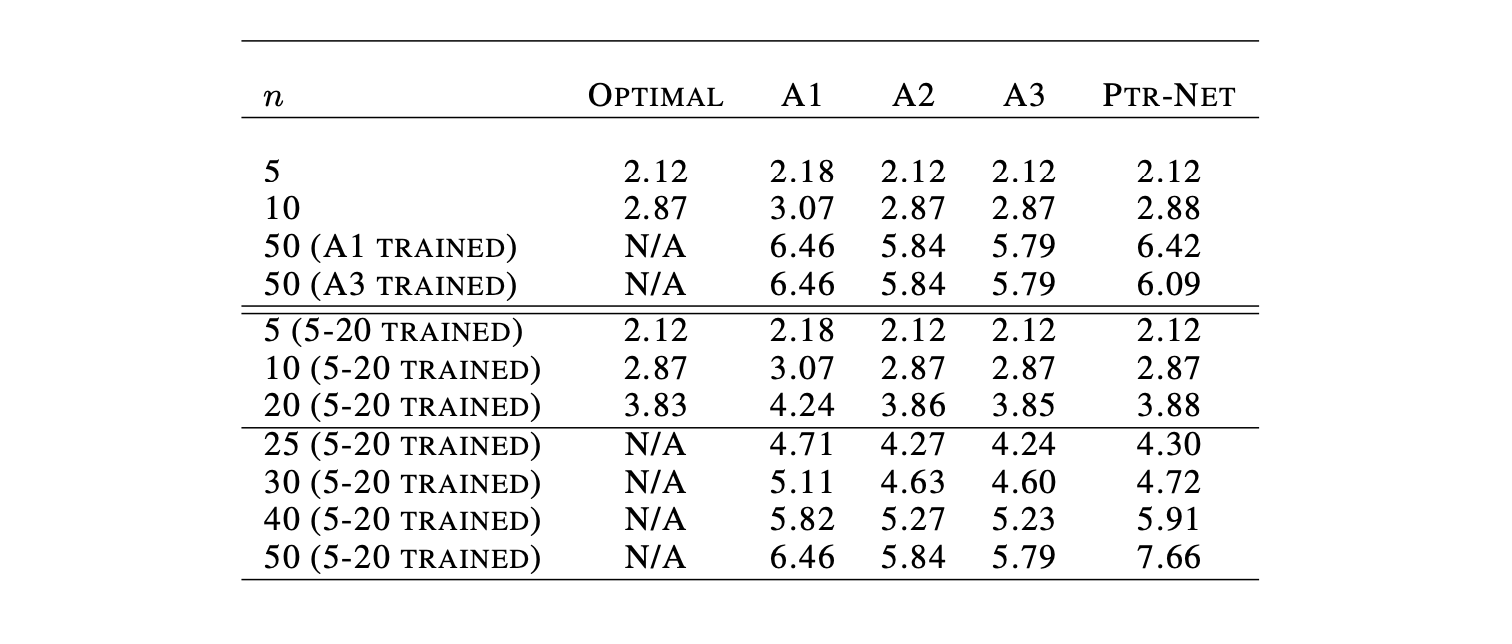 [테이블1] Pointer Network의 실험결과 (A1~A3: Baselines) [7]
[테이블1] Pointer Network의 실험결과 (A1~A3: Baselines) [7]
또한 Pointer Network는 TSP 뿐만 아니라 Convex Hull, Delaunay Triangulation 같은 다른 조합 최적화 문제에 대해서도 잘 동작한다는 사실이 실험을 통해 보여진 바가 있습니다.
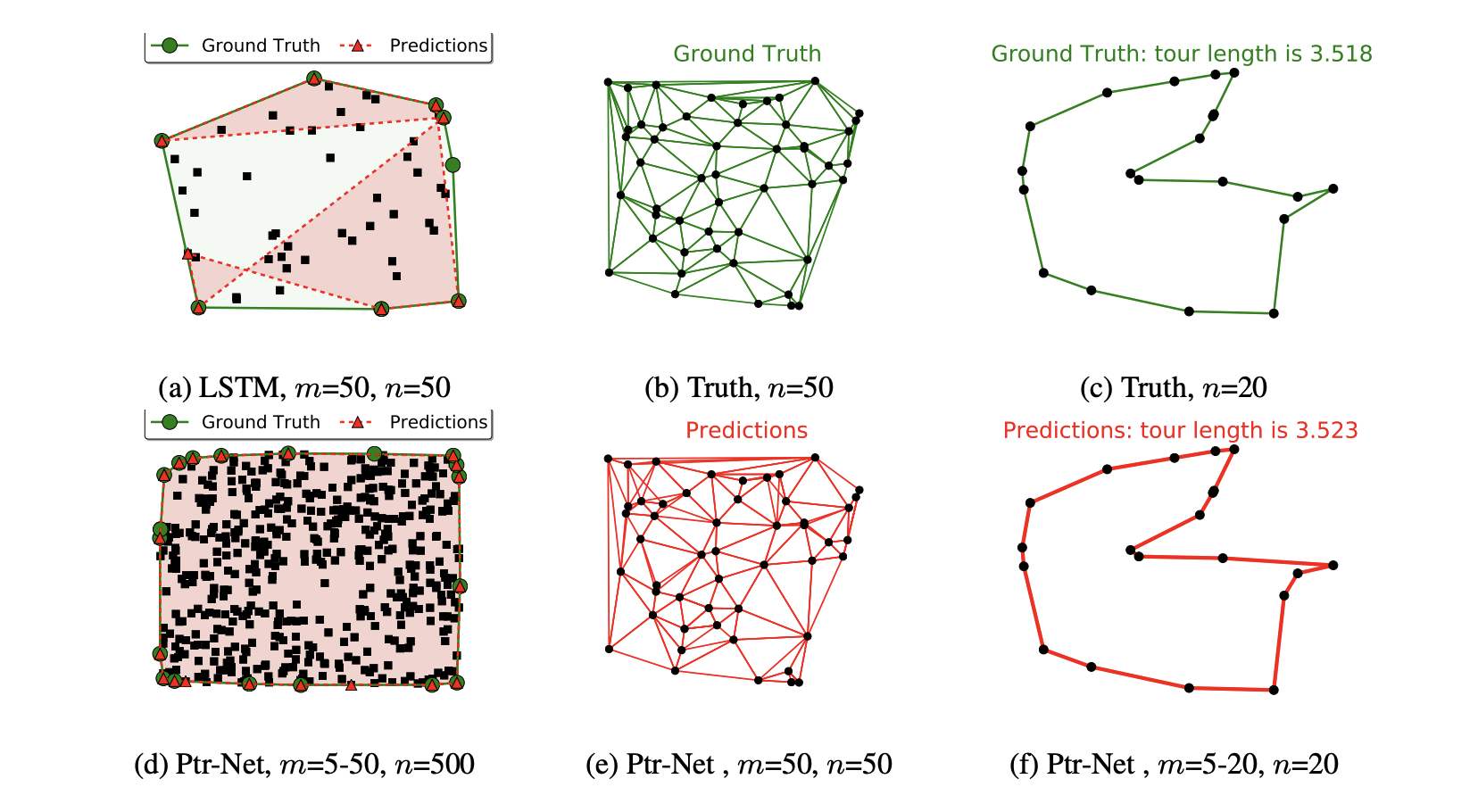 [그림4] Pointer Network의 실험결과: Convex hulls (좌), Delaunay (중앙) and TSP (우) [7]
[그림4] Pointer Network의 실험결과: Convex hulls (좌), Delaunay (중앙) and TSP (우) [7]
이처럼 다양한 문제에 대해 유연하게 잘 동작하는 구조라는 점에서 본 논문[1]의 저자들이 Pointer Network를 핵심적인 아이디어로 채택하였으며, 실험을 통해 Pointer Network에 강화학습이 적용된 방법론이 TSP 뿐만 아닌 Knapsack 문제에 대해서도 잘 동작함을 보입니다. (본 포스팅에서는 Knapsack 문제에 대한 내용은 생략하도록 하겠습니다.)
Policy Gradient (REINFORCE)
Policy는 강화학습 에이전트의 행동방식을 정의합니다. 이는 주어진 상태로부터 어떤 행동(Action)을 결정하는 상태-행동의 매핑함수라고도 할 수 있습니다. Policy Gradient는 주어진 문제에서 에이전트가 받는 보상의 기댓값을 최대화 하도록 Policy를 직접적으로 업데이트하는 방법들을 통칭하며, 이 중에서도 REINFORCE는 Monte-Carlo Method를 통해 얻은 샘플 에피소드로 추정한 리턴값을 이용해 Policy를 업데이트하는 방법입니다 [8].
본 논문에서 여행거리의 총 합은 모든 방문노드의 이전 방문노드와의 거리 총합과 마지막 방문노드와 시작 노드 거리의 합으로 정의합니다. 그리고 총 여행거리에 대한 기댓값을 목적함수(J)로 정의하고 이를 최소화시키는 것으로 문제를 정의합니다.
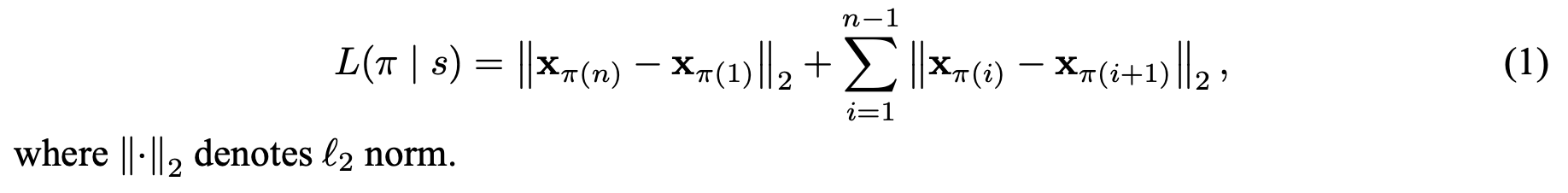
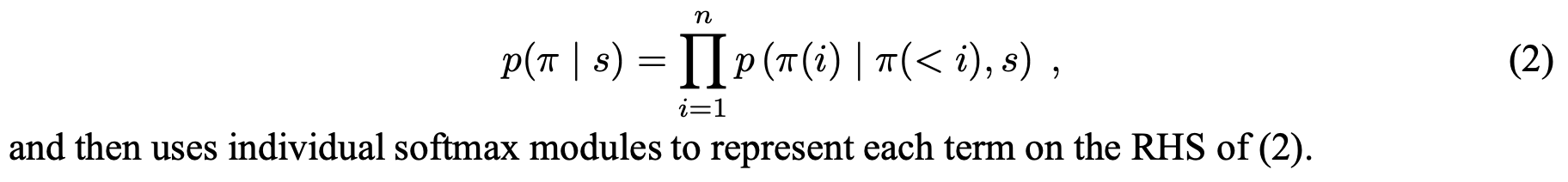
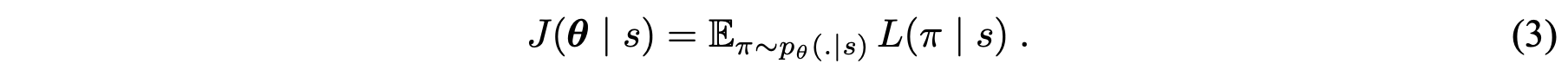
또한 REINFORCE 알고리즘으로 목적함수의 그레디언트를 표현하고 이를 Monte Carlo 샘플링 형태로 근사합니다. 더불어 총 여행거리의 기댓값을 예측하는 네트워크를 베이스라인 함수 $b(s)$를 정의합니다.
(Policy Grandient와 REINFORCE + Baseline에 대한 자세한 설명은 Lilian Weng의 블로그 포스팅을 참고해주세요.)
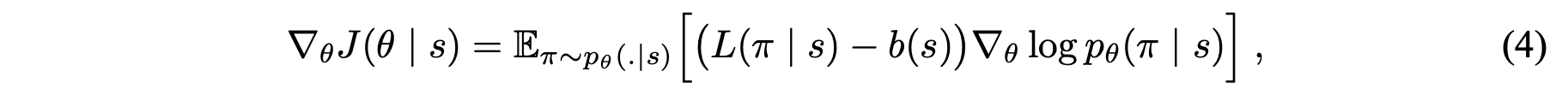
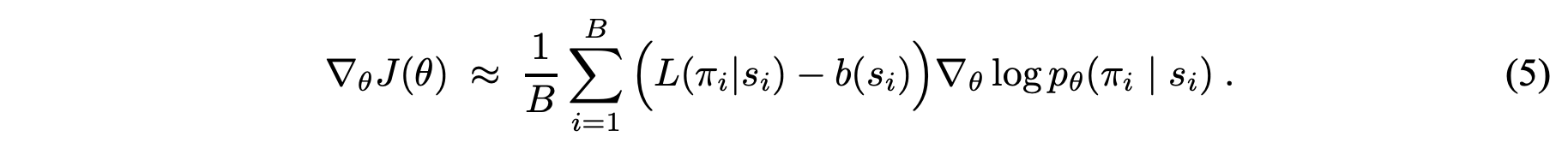
Experimental Results
저자는 다음과 같은 네 가지의 실험 설정을 제안합니다.
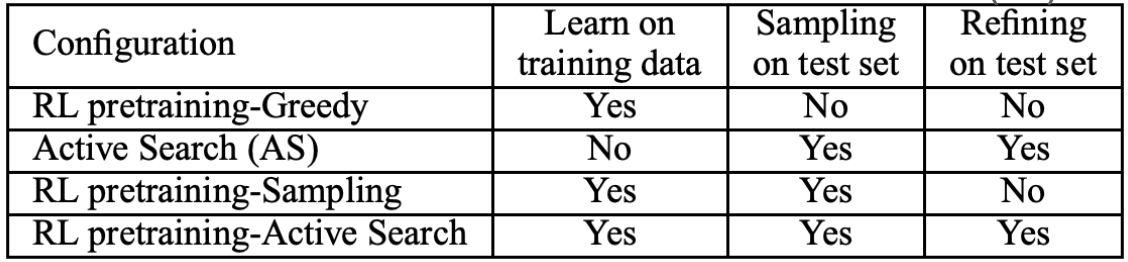 [테이블2] 4 가지 실험 설정 [1]
[테이블2] 4 가지 실험 설정 [1]
각각이 의미하는 바는 다음과 같습니다.
- RL pretraining-Greedy: 임의로 생성한 다수의 TSP 문제(학습을 위해 임의로 생성한 학습 데이터)에서 RL 에이전트를 학습시키며, 테스트에서는 RL 에이전트가 평가하는 가장 좋은 Action을 선택합니다.
- Active Search (AS): 학습 데이터에서의 학습 없이 테스트 데이터(1,000개의 임의의 TSP, LK-H[9]로 최적해 계산)에서 얻은 여러 샘플 경로들에 대해 더 작은 Loss를 갖게끔 Policy를 개선합니다.
- RL pretraining-Sampling: Training data에서 RL 에이전트를 학습시키며, 테스트 데이터에서 Stochastic Policy를 이용해 다양한 샘플 경로를 획득하고 그 중 가장 좋은 경로를 고르는 방법입니다.
- RL pretraining-Active Search (AS): 학습 데이터에서 RL 에이전트를 학습시키며, 테스트 데이터에서 Active Search를 하는 방법입니다. ($\star$)
결과적으로 20~100개 노드의 TSP에 대해 최적경로과 유사한 경로를 획득할 수 있었습니다.
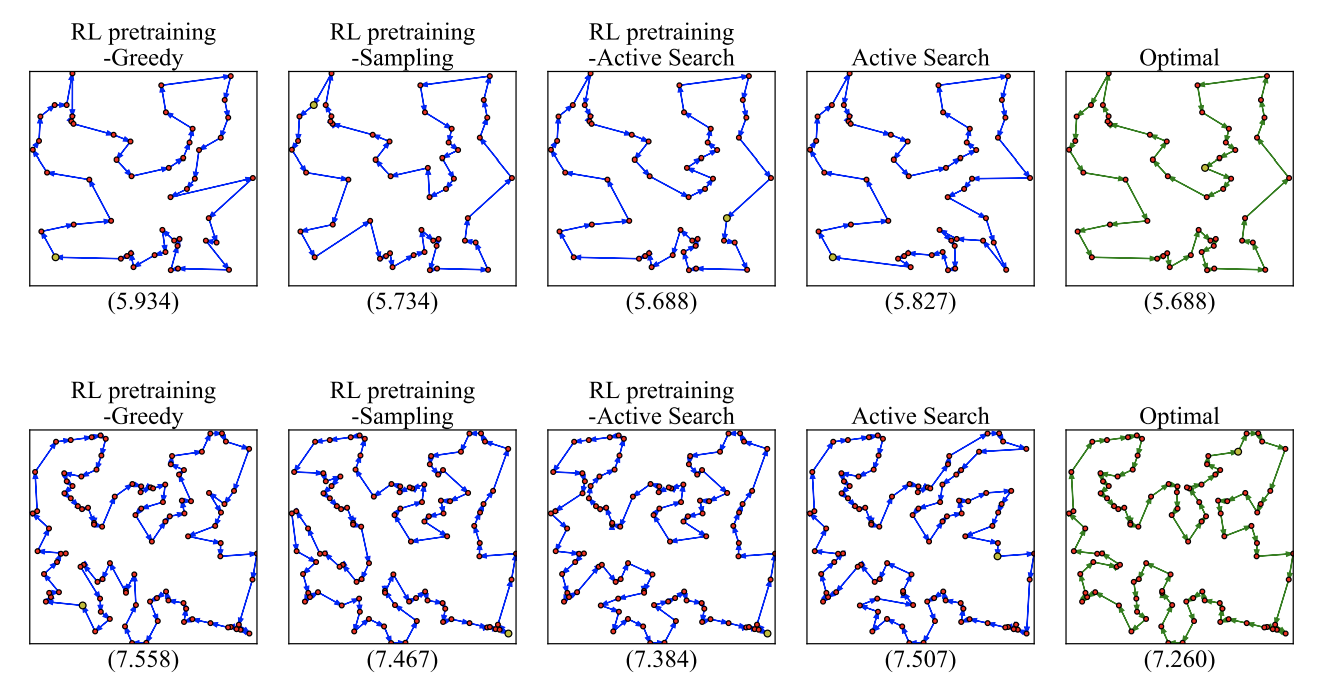 [그림5] 위: TSP50 / 아래: TSP100 (각 그림 아래 숫자는 총 여행거리를 의미) [1]
[그림5] 위: TSP50 / 아래: TSP100 (각 그림 아래 숫자는 총 여행거리를 의미) [1]
Related Posts
다음 포스팅에서 강화학습을 사용한 Neural Combinatorial Optimization 방법을 실제 산업 문제에 적용한 사례에 대해 알아보도록 하겠습니다.
- Chip Placement on FPGA 프로젝트를 소개합니다! (written by 우경민)
- Chip Placement with Deep Reinforcement Learning (written by 우경민)
References
[1] I. Bello, H. Pham, Q. V. Le, M. Norouzi, and S. Bengio, “Neural combinatorial optimization with reinforcement learning,” 2016.
[2] DocP’s Channel, “Travelling Salesman Problem (TSP): Direct sampling vs simulated annealing in Python,” 2017.
[3] WikiPedia, “Travelling Salesman Problem,” 12 Feb. 2021.
[4] David L Applegate, Robert E Bixby, Vasek Chvatal, and William J Cook. “The traveling salesman problem: a computational study,” Princeton university press, 2011.
[5] Barret Zoph and Quoc Le. “Neural architecture search with reinforcement learning,” arXiv preprint arXiv:1611.01578, 2016.
[6] Ilya Sutskever, Oriol Vinyals, and Quoc V. Le. “Sequence to sequence learning with neural networks,” In Advances in Neural Information Processing Systems, pp. 3104–3112, 2014.
[7] Oriol Vinyals, Meire Fortunato, and Navdeep Jaitly. “Pointer networks,” In Advances in Neural Information Processing Systems, pp. 2692–2700, 2015b.
[8] Ronald Williams. “Simple statistical gradient following algorithms for connectionnist reinforcement learning,” In Machine Learning, 1992.
[9] S. Lin and B. W. Kernighan. An effective heuristic algorithm for the traveling-salesman problem. Operations Research, 21(2):498–516, 1973.
» 이 글은 마키나락스 미디엄에 게재된 포스팅으로 원문은 여기서 확인하실 수 있습니다.
